mst: Euclidean and Mutual Reachability Minimum Spanning Trees¶
Description¶
A Euclidean minimum spanning tree (MST) provides a computationally convenient representation of a dataset: the \(n\) points are connected via \(n-1\) shortest segments. Provided that the dataset has been appropriately preprocessed so that the distances between the points are informative, an MST can be applied in outlier detection, clustering, density estimation, dimensionality reduction, and many other topological data analysis tasks.
Usage¶
mst(d, ...)
## Default S3 method:
mst(
d,
M = 0L,
distance = c("euclidean", "l2", "manhattan", "cityblock", "l1", "cosine"),
verbose = FALSE,
...
)
## S3 method for class 'dist'
mst(d, M = 0L, verbose = FALSE, ...)
Arguments¶
|
either a numeric matrix (or an object coercible to one, e.g., a data frame with numeric-like columns) or an object of class |
|
further arguments passed to |
|
smoothing factor; \(M=0\) selects the requested |
|
metric used in the case where |
|
logical; whether to print diagnostic messages and progress information |
Details¶
If d is a matrix and the Euclidean distance is requested (the default), then the MST is computed via a call to mst_euclid from quitefastmst. It is efficient in low-dimensional spaces. Otherwise, a general-purpose implementation of the Jarník (Prim/Dijkstra)-like \(O(n^2)\)-time algorithm is called.
If \(M>0\), then the minimum spanning tree is computed with respect to a mutual reachability distance (Campello et al., 2013): \(d_M(i,j)=\max(d(i,j), c_M(i), c_M(j))\), where \(d(i,j)\) is an ordinary distance and \(c_M(i)\) is the core distance given by \(d(i,k)\) with \(k\) being \(i\)’s \(M\)-th nearest neighbour (not including self, unlike in Campello et al., 2013). This pulls outliers away from their neighbours.
If the distances are not unique, there might be multiple trees spanning a given graph that meet the minimality property.
Value¶
Returns a numeric matrix of class mst with \(n-1\) rows and three columns: from, to, and dist. Its \(i\)-th row specifies the \(i\)-th edge of the MST which is incident to the vertices from[i] and to[i] with from[i] < to[i] (in \(1,...,n\)) and dist[i] gives the corresponding weight, i.e., the distance between the point pair. Edges are ordered increasingly with respect to their weights.
The Size attribute specifies the number of points, \(n\). The Labels attribute gives the labels of the input points, if available. The method attribute provides the name of the distance function used.
If \(M>0\), the nn.index attribute gives the indexes of the M nearest neighbours of each point and nn.dist provides the corresponding distances, both in the form of an \(n\) by \(M\) matrix.
References¶
V. Jarník, O jistem problemu minimalnim (z dopisu panu O. Borůvkovi), Prace Moravske Prirodovedecke Spolecnosti 6, 1930, 57-63
C.F. Olson, Parallel algorithms for hierarchical clustering, Parallel Computing 21, 1995, 1313-1325
R. Prim, Shortest connection networks and some generalisations, The Bell System Technical Journal 36(6), 1957, 1389-1401
O. Borůvka, O jistém problému minimálním, Práce Moravské Přírodovědecké Společnosti 3, 1926, 37–58
J.L. Bentley, Multidimensional binary search trees used for associative searching, Communications of the ACM 18(9), 509–517, 1975, doi:10.1145/361002.361007 W.B. March, R. Parikshit, A. Gray, Fast Euclidean minimum spanning tree: Algorithm, analysis, and applications, Proc. 16th ACM SIGKDD Intl. Conf. Knowledge Discovery and Data Mining (KDD ‘10), 2010, 603–612
R.J.G.B. Campello, D. Moulavi, J. Sander, Density-based clustering based on hierarchical density estimates, Lecture Notes in Computer Science 7819, 2013, 160-172, doi:10.1007/978-3-642-37456-2_14
M. Gagolewski, quitefastmst, in preparation, 2026, TODO
See Also¶
The official online manual of deadwood at https://deadwood.gagolewski.com/
Examples¶
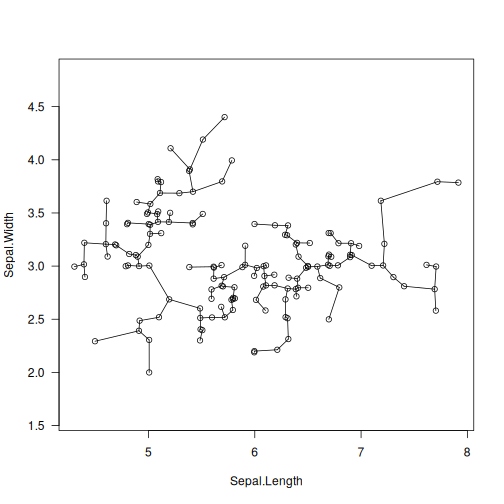
library("datasets")
data("iris")
X <- jitter(as.matrix(iris[1:2])) # some data
T <- mst(X)
plot(X, asp=1, las=1)
segments(X[T[, 1], 1], X[T[, 1], 2],
X[T[, 2], 1], X[T[, 2], 2])